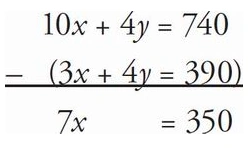The 2024 SAT standardized test is a critical assessment for college admissions. The math section covers a wide range of topics. To help students prepare, we’ve created a practice paper. This paper includes various math problems to help students become familiar with the test format and excel in their exam.
1.
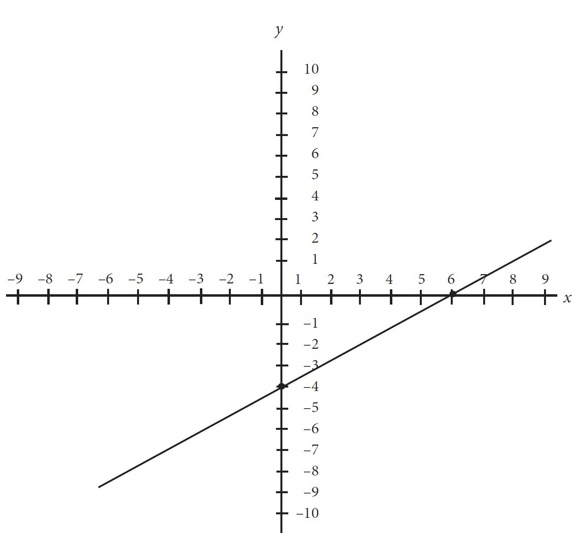
The graph, y = f(x), shown above models the performance of a certain crop, where x is the nutrients subtracted or added to the soil and y is the gain or loss of pieces of fruit added to the total harvest. A more powerful fertilizer that is used causes the graph y = f(x) to be reflected over the line y = x. Which of the following best describes the behavior of the crop with the new fertilizer?
A. For every three nutrients added to the soil, the crop loses two additional fruits for the total harvest.
B. For every two nutrients added to the soil, the crop loses two additional fruits for the total harvest.
C. For every three nutrients added to the soil, the crop adds two additional fruits to the total harvest.
D. For every two nutrients added to the soil, the crop adds three additional fruits to the total harvest.
2. George and Joe both interview the same 20 fellow students regarding their interest in their school’s new Model UN Club. George asked the students to respond with Interested, Sort of Interested, and Not Interested. Joe asked the students to rate their interest on a scale of 1 to 5. The results of the polls are below.
George’s Poll
Response Number of Students Interested 8 Sort of Interested 5 Not Interested 7
Joe’s Poll
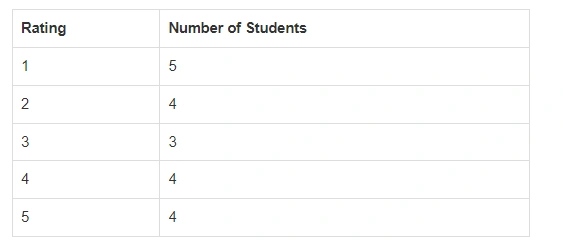
After reviewing the data, the Model UN advisors determine that Joe neglected to include whether a 1 or 5 was the best rating in his report. What additional piece of information would most help the advisor determine whether a 1 or 5 was the best rating?
A. Requesting that George redo his poll with the same rating system as Joe’s poll.
B. Requesting that Joe redo his poll with the same rating system as George’s poll.
C. Polling all of the students who said “Interested” in George’s Poll and asking them to choose between “Extremely Interested” and “Very Interested.”
D. Polling all of the students who gave a “1” rating in Joe’s poll and ask them if they are interested in Model UN.
3. Each winter, Captain Dan’s Ski Lodge rents both pairs of skis and snowboards to its guests for a flat daily rate per pair of skis and a flat daily rate per snowboard. Five pairs of skis and two snowboards will cost a family $370. Three pairs of skis and four snowboards will cost a family $390. During a particularly slow season, Captain Dan announces a 10% discount on all skis and snowboards. What would be the cost of renting two pairs of skis and two snowboards if they were rented during this discount period?
A. $99
B. $110
C. $198
D. $220
4. If 8x + 8y = 18 and x² – y² = \( -\frac{3}{8} \), what is the value of 2x – 2y ?
A. \( -\frac{1}{3} \)
B. \( -\frac{1}{6} \)
C. \( \frac{1}{3} \)
D. \( \frac{1}{6} \)
5. Shaun is developing a weight loss regimen, which includes both a workout plan and a calorie-restriction plan. Shaun wants to work out for no less than 30 minutes and no more than 60 minutes a day and consume no less than 2,000 and no more than 2,500 calories. If each minute, m, of his workout time burns 50 calories, which of the following inequalities represents the number of minutes, m, that Shaun can work out each day to burn off as many calories as he consumes?
A. 30 ≤ m ≤ 60
B. 30 ≤ m ≤ 50
C. 40 ≤ m < 50
D. 40 ≤ m ≤ 50
Warning: Undefined variable $in_same_cat in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
Warning: Undefined variable $excluded_categories in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27

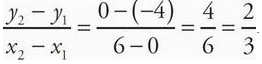 . When this line is reflected across the line y = x, the x and y values switch, so the new slope would be the reciprocal of the original slope. Since our original slope was
. When this line is reflected across the line y = x, the x and y values switch, so the new slope would be the reciprocal of the original slope. Since our original slope was