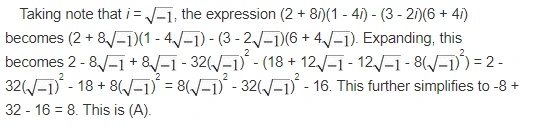6. If x² + 2xy + y² = 64 and y – x = 12, which of the following could be the value of x ?
A. -10
B. -4
C. 2
D. 10
7. Samantha offers two different packages of yoga classes at her yoga studio. She offers two hot yoga sessions and three zero gravity yoga sessions at a total cost of $400. She also offers four hot yoga sessions and two zero gravity sessions at a price of $440. Samantha wants to offer a larger package for long-time clients in which the cost must exceed $800. If Samantha does not wish to include more than 13 sessions for the long-time client package, will she be able to create this package for her clients?
A. No, because the closest package that she can offer consists of three hot yoga and three zero gravity yoga sessions.
B. No, because the closest package that she can offer consists of four hot yoga and four zero gravity yoga sessions.
C. Yes, because she can offer five hot yoga and five zero gravity yoga sessions.
D. Yes, because she can offer six hot yoga and six zero gravity yoga sessions.
8. Cuthbert is conducting a chemistry experiment that calls for a number of chemicals to be mixed in various quantities. The one amount of which he is unsure is grams of potassium, p . If Cuthbert is certain that (3p2 + 14p + 24) – 2(p2 + 7p + 20) = 0, what is one possible value of 3p + 6, the exact number of grams of potassium that Cuthbert would like to use for this experiment?
A. 20
B. 18
C. 12
D. 10
9. What is the value of (2 + 8i)(1 – 4i) – (3 – 2i)(6 + 4i) ?
(Note: i = \sqrt[]{-1} )
A. 8
B. 26
C. 34
D. 50
10. If 2\sqrt[]{x} = x – 3, which of the following is the solution set for x ?
A. {-1, 9}
B. {1, -9}
C. {9}
D. {1, 9}
Warning: Undefined variable $in_same_cat in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
Warning: Undefined variable $excluded_categories in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27