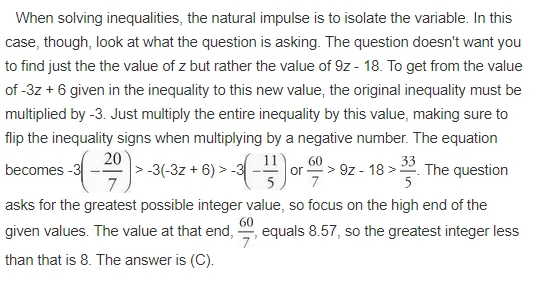2024 SAT Standardized Test Math Practice Paper 4

The 2024 SAT standardized test is a critical assessment for college admissions. The math section covers a wide range of topics. To help students prepare, we’ve created a practice paper. This paper includes various math problems to help students become familiar with the test format and excel in their exam.

 

1. Bryan, who works in a high-end jewelry store, earns a base pay of $10.00 per hour plus a certain percent commission on the sales that he helps to broker in the store. Bryan worked an average of 35 hours per week over the past two weeks and helped to broker sales of $5,000.00 worth of jewelry during that same two-week period. If Bryan’s earnings for the two-week period were $850.00, what percent commission on sales does Bryan earn?

A. 1%
B. 2%
C. 3%
D. 4%

Correct Answer: C

Answer Explanation:

There are a few different ways to approach this question. In any approach, the best first step is to figure out how much income Bryan earned during the two-week period without the commission. Since he worked an average of 35 hours per week for two weeks, he worked a total of 70 hours. At a rate of $10.00 per hour base pay, this would add up to $700.00 (70 × 10 = 700). Since Bryan’s earnings were actually $850.00, that means he must have earned $150.00 of commission (850 – 700 = 150). At this point, you can calculate the percent commission algebraically or simply work backwards from the answers. Algebraically, you know that $150.00 is equal to a certain percent of $5,000.00 in sales, which can be represented as follows: 150 = (5,000). Solve for x, and you get 3, which is (C). If instead you wish to work backwards from the answers, you can take the answers and calculate what 1%, 2%, etc. of $5,000.00 would be, and then add that back to $700.00 to see which choice matches your target of $850.00: (C).

2. If ​ \frac{(C+x)}{x-3}=\frac{x+8}{3} ​, which of the following could be an expression of C in terms of x ?

Math sat 3 1

Correct Answer: C

Answer Explanation:

Cross-multiply to get 3(C + x) = (x – 3)(x + 8). Expand the right side of the equation to get 3(C + x) = x2 + 5x – 24. Distribute the 3 to get 3C + 3x = x2 + 5x – 24. Subtract 3x from both sides of the equation to get 3C = x² + 2x – 24. Factor the right side of the equation to get 3C = (x + 6)(x – 4). Divide both sides by 3 to get C =​ \frac{(x+6)(x-4)}{3} ​ = ​ \frac{1}{3}(x + 6)(x – 4) . The correct answer is (C).

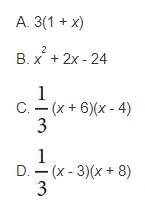
3. Lennon has 6 hours to spend in  Ha Ha Tonka State Park. He plans to drive around the park at an average speed of 20 miles per hour, looking for a good trail  to hike. Once he finds a trail he likes, he will spend the remainder of his time hiking it. He hopes to travel more than 60 miles total while in the park. If he hikes at an average speed of 1.5 miles per hour, which of the following systems of inequalities can be solved for the number of hours Lennon spends driving, d, and the number of hours he spends hiking, h, while he is at the park?

A. 1.5h + 20d > 60
h + d ≤ 6
B. 1.5h + 20d > 60
h + d ≥ 6
C. 1.5h + 20d < 60
h + d ≥ 360
D. 20h + 1.5d > 6
h + d ≤ 60

Correct Answer: A

Answer Explanation:

Start with the easiest piece of information first, and use Process of Elimination. Given that h is the number of hours spent hiking and d is the number of hours driving, the total number of hours Lennon spends in the park can be calculated as h + d. The question states that Lennon has up to 6 hours to spend in the park-“up to” means ≤. So, h + d ≤ 6. Eliminate (B), (C), and (D). The correct answer is (A).

4. In a certain sporting goods manufacturing company, a quality control expert tests a randomly selected group of 1,000 tennis balls in order to determine how many contain defects. If this quality control expert discovered that 13 of the randomly selected tennis balls were defective, which of the following inferences would be most supported?

A. 98.7% of the company’s tennis balls are defective
B. 98.7% of the company’s tennis balls are not defective
C. 9.87% of the company’s tennis balls are defective
D. 9.87% of the company’s tennis balls are not defective

Correct Answer: B

Answer Explanation:

The quality control expert discovered that 13 out of 1,000 randomly selected tennis balls were defective.​ \frac{13}{1000} ​ = 0.013, which is equivalent to 1.3%. This means that 100 – 1.3 = 98.7% of tennis balls tested were not defective, and this data most supports answer (B).

5. If ​ -\frac{20}{7} ​ < -3z + 6 < ​ -\frac{11}{5} ​ , what is the greatest possible integer value of 9z – 18 ?

A. 6
B. 7
C. 8
D. 9

Correct Answer: C

Answer Explanation:

Math sat 3 2

Pages: 1 2

Warning: Undefined variable $in_same_cat in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27

Warning: Undefined variable $excluded_categories in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
< PREVIOUS POST2024 SAT Standardized Test Math Practice Paper 3
NEXT POST >2024 SAT Standardized Test Math Practice Paper 5

Leave A Comment?