2024 SAT Standardized Test Math Practice Paper 32

The 2024 SAT standardized test is a critical assessment for college admissions. The math section covers a wide range of topics. To help students prepare, we’ve created a practice paper. This paper includes various math problems to help students become familiar with the test format and excel in their exam.

 

1.

Sat math 32 1

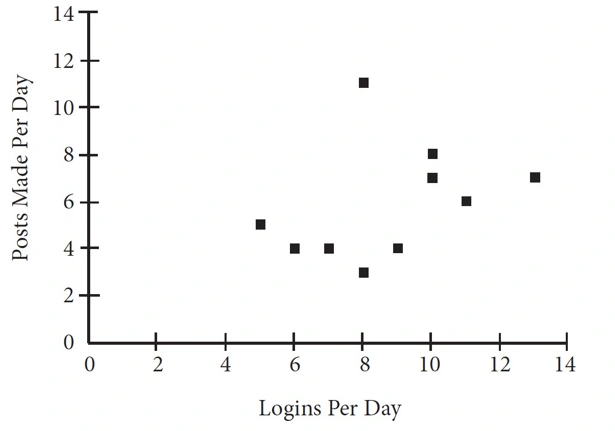
Given the scatterplot graph above, ten students at Welton Academy were polled at random about their usage of the school’s new physics-centered social media app, E = MC Shared. The app was developed to encourage students to discuss physics curricula and concepts in ways that mirrored social media trends in 2013. Students were asked how many times they logged into the app each day as well as how many posts they actually made using the app. With the given data, what conclusions can be drawn about this group of students?

A. The majority of students polled logged in more times per day than they posted.
B. The majority of students polled posted more times per day than they logged in.
C. The majority of students polled logged in and posted an equal number of times.
D. No relationship can be drawn between logins per day and posts per day.

Correct Answer: A

Answer Explanation:

The best way to approach this question is through POE. Choice (A) states that the majority of students polled logged in more times than they posted. The values along the x-axis of the graph are, for most of the data points, higher than the values along the y-axis of the graph, and thus (A) is true according to the data provided. This same data contradicts (B) and (C). You can eliminate (D) because the data does, in fact, allow you to draw a conclusion about the relationship between the variables.

2.

Sat math 32 2

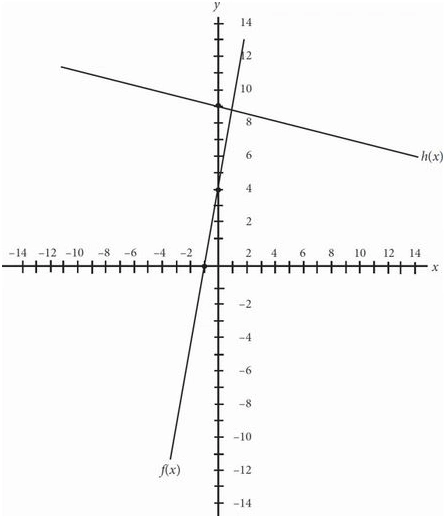
Two graphs, f(x) and h(x), are shown above. If f(x) = 3x + 4 and f(x) and h(x) are perpendicular, which of the following could be the equation of h(x) ?

A. h(x) = ​\( \frac{1}{3} \)​x + 9
B. h(x) = ​\( -\frac{1}{3} \)​x + 9
C. h(x) = 3x + 9
D. h(x) = -3x + 9

Correct Answer: B

Answer Explanation:

Don’t get too thrown off by the graph. All you need to know to solve this question is that perpendicular lines have slopes that are the negative reciprocals of each other. Since the standard equation for a line is y = mx + b, the slope of the f(x) line is 3. The slope of the h(x) line must therefore be ​\( \frac{1}{3} \)​. The only answer choice that matches is (B).

3. The number of eggs that Farmer Jones has in his  chicken coop will grow exponentially as Farmer Jones buys more chickens to increase production. The number of eggs Farmer Jones has in the coop can be modeled by the equation y = ​\( 3^x \)​ beginning on Day 1, where x is given by x = 1, and y is the number of eggs currently in the coop. If the coop can support only 4,000 eggs, and Farmer Jones empties the coop every day, on which day will the chickens produce too many eggs for the coop to support?

A. Day 6
B. Day 7
C. Day 8
D. Day 9

Correct Answer: C

Answer Explanation:

The best way to deal with this question is to Plug in the Answers (PITA), starting with (A). If x = 6, then y = ​\( 3^6 \)​ = 729. This is less than 4,000, so eliminate (A) and move to the next answer choice. If x = 7, then y = ​\( 3^7 \)​ = 2,187. This is still less than 4,000, so eliminate (B). If x = 8, then y = ​\( 3^8 \)​ = 6,561. This is greater than 4,000, so (C) must be the correct answer.

4. If a = ​\( \frac{4a²}{16} \)​and a is a nonzero integer, which of the following is equivalent to a ?

A. 4a
B. 4​\( \sqrt[]{a} \)​
C. ​\( \sqrt[]{2a} \)​
D. 2​\( \sqrt[]{a} \)​

Correct Answer: D

Answer Explanation:

The first step here is to simplify the equation and solve for a. Start by multiplying both sides by 16 to get 16a = 4a². Divide both sides by 4 to get 4a = a². Divide both sides by a to get 4 = a. This is now your target answer. Plug a = 4 into the values of a in the answer choices to determine which one matches 4. Choice (D) is the answer, since 2​\( \sqrt[]{a} \)​ = 2​\( \sqrt[]{4} \)​ = 2(2) = 4.

5. Three different chefs work together to prepare meals for 280 dinner guests. Each works at a different speed, and their combined output throughout the night is modeled by the equation 8x + 4x + 2x = 280. If x is a positive integer, which of the following could 8x represent in the equation?

A. The total meal output by the slowest chef, who made 40 meals.
B. The total meal output by the fastest chef, who made 160 meals.
C. The total meal output by the fastest chef, who made 80 meals.
D. The difference between the output between the slowest and fastest chef, which would be 120 meals.

Correct Answer: B

Answer Explanation:

Since work = rate × time, the 280 in the equation must represent the total number of meals (i.e. the “work”). All three chefs are working together, so they work for the same amount of time, and x must represent that time. The coefficients 8, 4, and 2 must therefore represent the chefs’ respective rates, or how many meals each prepares in a set amount of time. Since 8 is the greatest of these three coefficients, 8x must be the meal output of the fastest chef, either (B) or (C). Now you need to solve the equation: 8x + 4x + 2x = 280. Combining like terms gives you 14x = 280. Divide both sides by 14 to determine that x = 20. This number represents the amount of time that the chefs worked, so the actual number of meals prepared by the fastest chef would be 8 × 20 = 160 meals, which is (B).

Pages: 1 2

Warning: Undefined variable $in_same_cat in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27

Warning: Undefined variable $excluded_categories in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
< PREVIOUS POST2024 SAT Standardized Test Math Practice Paper 28
NEXT POST >2024 SAT Standardized Test Math Practice Paper 33

Leave A Comment?