6. In the 1990s, the park rangers at Yellowstone National Park implemented a program aimed at increasing the dwindling coyote population in Montana. Results of studies of the coyote population in the park are shown in the scatterplot below.
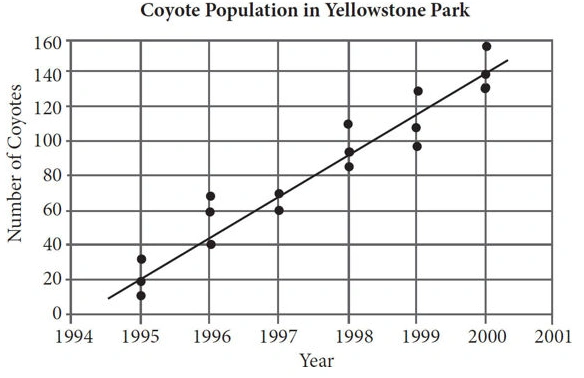
Based on the line of best fit in the scatterplot above, which of the following is the closest to the average annual increase in coyotes in Yellowstone Park between 1995 and 2000 ?
A. 22
B. 24
C. 26
D. 28
7.
In the 1990s, the park rangers at Yellowstone National Park implemented a program aimed at increasing the dwindling coyote population in Montana. Results of studies of the coyote population in the park are shown in the scatterplot below.

According to the data in the scatterplot, which of the following best represents the percent increase between the median of the results of the studies from 1995 and the median of the results of the studies from 1996 ?
A. 50%
B. 100%
C. 150%
D. 200%
8. Bailey’s Boutique Clothing is having a 20% off sale during which shirts cost $30.00 and pants cost $60.00. On the day of the sale, Bailey’s sells \( \frac{2}{3} \)a total of 60 shirts and pants and earned a total of $2,250. On a regular day, Bailey’s sellsthe number of shirts and pants sold during the sale and earns a total of $1,875. Solving which of the following systems of equations yields the number of shirts, s, and the number of pants, p, sold during a regular day?
A. s + p = 40
37.5s + 75p = 1,875
B. s + p = 40
30s + 60p = 2,250
C. s + p = 60
30s + 60p = 2,250
D. s + p = 2,250
30s + 60p = 60
9. Bryan, who works in a high-end jewelry store, earns a base pay of $10.00 per hour plus a certain percent commission on the sales that he helps to broker in the store. Bryan worked an average of 35 hours per week over the past two weeks and helped to broker sales of $5,000.00 worth of jewelry during that same two-week period. If Bryan’s earnings for the two-week period were $850.00, what percent commission on sales does Bryan earn?
A. 1%
B. 2%
C. 3%
D. 4%
10. Lennon has 6 hours to spend in Ha Ha Tonka State Park. He plans to drive around the park at an average speed of 20 miles per hour, looking for a good trail to hike. Once he finds a trail he likes, he will spend the remainder of his time hiking it. He hopes to travel more than 60 miles total while in the park. If he hikes at an average speed of 1.5 miles per hour, which of the following systems of inequalities can be solved for the number of hours Lennon spends driving, d, and the number of hours he spends hiking, h, while he is at the park?
A. 1.5h + 20d > 60
h + d ≤ 6
B. 1.5h + 20d > 60
h + d ≥ 6
C. 1.5h + 20d < 60
h + d ≥ 360
D. 20h + 1.5d > 6
h + d ≤ 60
Warning: Undefined variable $in_same_cat in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
Warning: Undefined variable $excluded_categories in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
