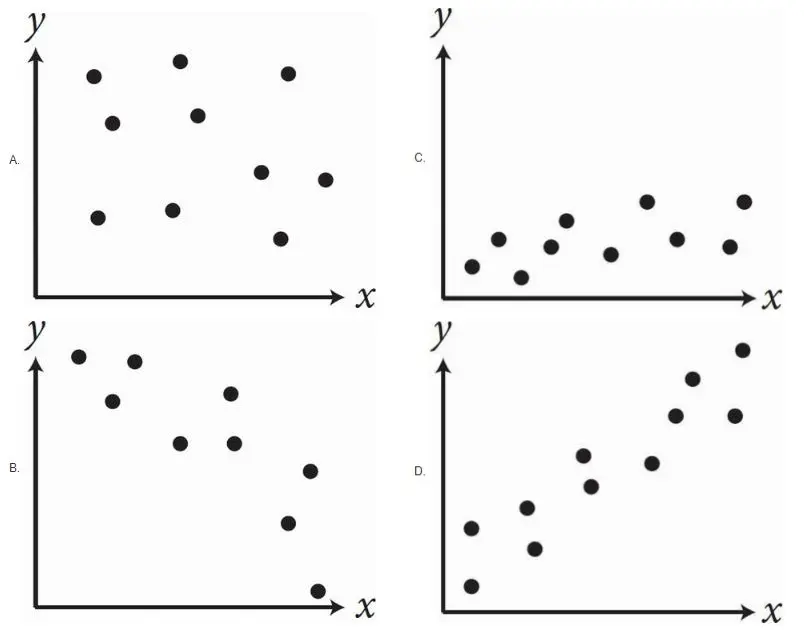
6. Which of the following graphs shows a strong positive association between x and y ?
7. If \( \sqrt[]{x} \)+ 22 = 38, what is the value of x ?
A. 4
B. 16
C. 32
D. 256
8. If each number in the following sum were increased by t, the new sum would be 4.22. What is the value of t ?
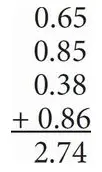
A. 0.24
B. 0.29
C. 0.33
D. 0.37
9. If x + 6 > 0 and 1 – 2x > -1, then x could equal each of the following EXCEPT
A. -6
B. -4
C. 0
D. \( \frac{1}{2} \)
10. If \( \frac{2x}{x²+1}=\frac{2}{x+2} \), what is the value of x ?
A. \( -\frac{1}{4} \)
B. \( \frac{1}{2} \)
C. 0
D. 2
Pages: 1 2
Warning: Undefined variable $in_same_cat in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
Warning: Undefined variable $excluded_categories in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
< PREVIOUS POST2024 SAT Standardized Test Math Practice Paper 19
