6.
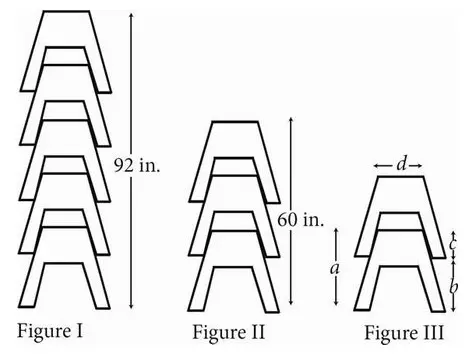
In figures I and II above, two stacks of identical carpenter’s sawhorses are shown, with heights of 92 and 60 inches, respectively. The height, in inches, of a stack of k sawhorses is given by the function h(k) = 16k + 12, where k is a positive integer and k ≥ 1. The number 12 in the function represents which of the dimensions shown in Figure III ?
A. a, the height of one sawhorse
B. b, the distance from the bottom of one sawhorse to the bottom of the next highest sawhorse
C. c, the distance from the top of one sawhorse to the bottom of the next highest sawhorse
D. d, the width of a sawhorse at the top
7.
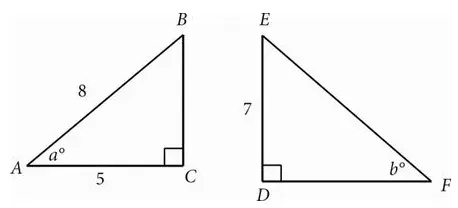
In the figure above, if sin a = cos b, which of the following is closest to the length of DF ?
A. 5.6
B. 8.7
C. 11.2
D. 12
8.
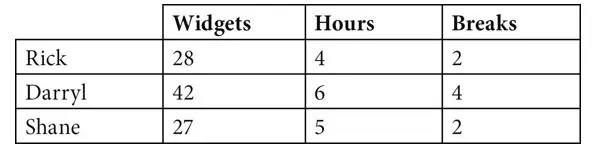
Rick, Shane, and Darryl work at a widget factory. The table above shows the number of hours they each spent at the factory on a given day, the number of widgets they produced, and the number of 15-minute breaks they took while they were at the factory. Each man works at a constant rate.
Rick and Shane are each assigned an equal number of widgets. Neither will take breaks in order to complete this assignment as quickly as possible. Rick offers to do a certain percentage of Shane’s assignment so that they both finish at the same time. What percentage of Shane’s original assignment does Rick do?
A. 12.50%
B. 14.30%
C. 16.70%
D. 25%
9.
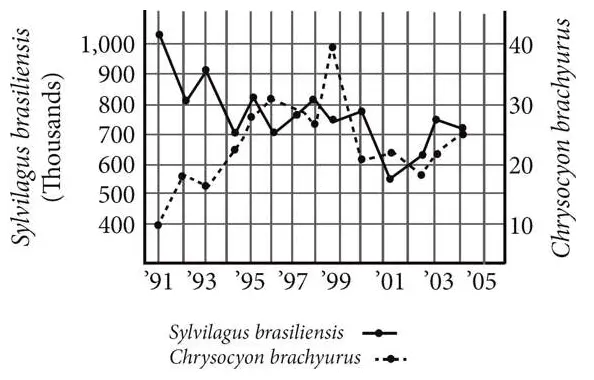
The graph above represents the effect of efforts to reintroduce Chrysocyon brachyurus, a wolf-like predator, to Uruguay. It tracks the population of both Chrysocyon brachyurus and Sylvilagus brasiliensis, the rabbit species that is a primary food-source.
For which of the following periods did the Sylvilagus brasiliensis population undergo the greatest percent decrease?
A. ’91-’92
B. ’93-’95
C. ’99-’00
D. ’00-’01
10. If cos θ = 1.66, then tan θ =?
A. 0.6
B. 0.76
C. 1.32
D. 1.76
Warning: Undefined variable $in_same_cat in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
Warning: Undefined variable $excluded_categories in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27

