2024 SAT Standardized Test Math Practice Paper 14

The 2024 SAT standardized test is a critical assessment for college admissions. The math section covers a wide range of topics. To help students prepare, we’ve created a practice paper. This paper includes various math problems to help students become familiar with the test format and excel in their exam.

 

1. V(t) = at + k

At a certain manufacturing plant, the total number of vacation days, V(t), an employee has accrued is given by the function above, where t is the number of years the employee has worked at the plant, and a and k are constants. If Martin has accrued 9 more vacation days than Emilio has, how many more years has Martin worked than Emilio?

A. ​\( \frac{9}{a} \)​
B. 9 – a
C. 9 + a
D. 9a

Correct Answer: A

Answer Explanation:

Whenever there are variables in the question and in the answers, think Plugging In. Let’s say that for Emilio a = 2, t = 4, and k = 10. Then Emilio’s accrued vacation days can be calculated as V(t) = 2(4) + 10 = 18. This means that Martin has accrued 18 + 9 = 27 vacation days. Because a and k are constants, their values do not change. The number of years that Martin has worked at the manufacturing plant can therefore be calculated as 27 = 2t + 10. Solve for t to get 17 = 2t or t =​\( \frac{17}{2} \)​ = 8.5. Therefore, Martin has worked 8.5 – 4 = 4.5 more years than Emilio. Plug 2 in for a in the answers to see which answer equals 4.5. Choice (A) becomes​\( \frac{9}{2} \)​ = 4.5. Keep (A) but check the remaining answers just in case. Choice (B) becomes 9 – 2 = 7, (C) becomes 9 + 2 = 11, and (D) becomes 9(2) = 19. Eliminate (B), (C), and (D). The correct answer is (A).

2.

Sat math 14 1

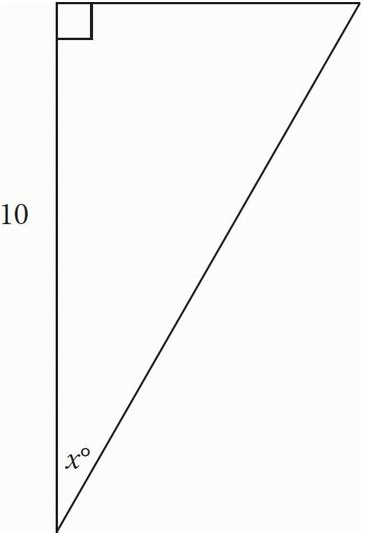
In the figure above, sin x° =​\( \frac{2\sqrt[]{29}}{29} \)​ . What is the perimeter of the figure?

A. 10 + ​\( \frac{2\sqrt[]{29}}{29} \)​
B. 7 + ​\( {\sqrt[]{29}} \)​
C. 14 + 2​\( {\sqrt[]{29}} \)​
D. 39 + 2​\( {\sqrt[]{29}} \)​

Correct Answer: C

3. At Santa Monica High School, the ratio of juniors to seniors is 4 to 3, the ratio of seniors to sophomores is 5 to 4, and the ratio of freshmen to sophomores is 7 to 6. What is the ratio of freshmen to seniors?

A. ​\( \frac{7}{3} \)​
B. ​\( \frac{5}{3} \)​
C. ​\( \frac{9}{7} \)​
D. ​\( \frac{14}{15} \)​

Correct Answer: D

4. David is planning a dinner for his birthday. At one restaurant, the cost per person for dinner is $15, with an additional one-time set-up charge of $35. David has a maximum budget of $150. If p represents the number of people (including David) who will attend the dinner, which of the following inequalities represents the number of people who can attend within budget?

A. 15p ≤ 150 + 35
B. 35 ≤ 150 – 15p
C. 15p ≥ 150 – 35
D. 35 ≥ 150 – 15p

Subtract the one-time set-up charge from David’s budget first: 150 – 35 = 115. Calculate the number of people David can invite as follows: 115 ÷ 15 = 7.6. David can invite at most 7 people (including himself), so p ≤ 7. In (A), 15p ≤ 185, so p ≤ 12.3 or p ≤ 12.3. Eliminate (A). Solve for p in (B) as follows: add 15p to both sides to get 15p + 35 ≤ 150, so 15p ≤ 115 and p ≤ 7.6. The correct answer is (B).

Correct Answer: B

Answer Explanation:

Subtract the one-time set-up charge from David’s budget first: 150 – 35 = 115. Calculate the number of people David can invite as follows: 115 ÷ 15 = 7.6. David can invite at most 7 people (including himself), so p ≤ 7. In (A), 15p ≤ 185, so p ≤ 12.3 or p ≤ 12.3. Eliminate (A). Solve for p in (B) as follows: add 15p to both sides to get 15p + 35 ≤ 150, so 15p ≤ 115 and p ≤ 7.6. The correct answer is (B).

5. When a virus breaks out, each infected person can infect multiple new people. In a particularly bad flu outbreak at an elementary school, the number of infected people triples each day in the first school week of January. If 5 people were sick with the flu on Monday, which of the following equations best predicts the number of infected people, I(d), d days after Monday?

A. I(d) = 5 × 3d²
B. I(d) = 5d³
C. I(d) = 5 × ​\( 3^d \)​
D. I(d) = 5 × 9d

Correct Answer: C

Answer Explanation:

Whenever there are variables in the question and in the answer choices, think Plugging In. Let d = 2. On the first day after Monday, 5 × 3 = 15 people will be infected. On the second day after Monday, 15 × 3 = 45 people will be infected. Therefore, when d = 2, the result is 45. Plug 2 in for d in the answer choices to see which answer equals the target number of 45. Choice (A) becomes 5 × 3(2²) = 5 × 12 = 60. This does not match the target number, so eliminate (A). Choice (B) becomes 5 × 2³ = 40. Eliminate (B). Choice (C) becomes 5 × 3² = 45. Keep (C), but check the remaining choice just in case. Choice (D) becomes 5 × 9(5) = 225. Eliminate (D), and choose (C).

Pages: 1 2

Warning: Undefined variable $in_same_cat in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27

Warning: Undefined variable $excluded_categories in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
< PREVIOUS POST2024 SAT Standardized Test Math Practice Paper 13
NEXT POST >2024 SAT Standardized Test Math Practice Paper 15

Leave A Comment?