2024 SAT Standardized Test Math Practice Paper 12

6. The cost in dollars, C, of producing a custom-made T-shirt with a team logo is given by the formula C = 110 +​\( \frac{x}{2} \)​ , where x is the number of T-shirts produced. When every T-shirt produced is sold, the revenue from selling the customized T-shirts is given by R = 15x – ​\( \frac{x²}{10} \)​. Which one of the following would be the formula for the profit from producing and selling x T-shirts?
(Profit = Revenue – Cost)

Math 12 4

Correct Answer: C

Answer Explanation:

Math 12 5

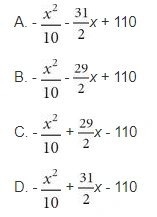
7. While on vacation in Morocco, Erik decided to splurge on a fancy hotel that cost 2,000 Moroccan dirhams per night. If he stayed in that particular hotel for three nights, but his bank only lets him withdraw $200 at a time, how many visits to the ATM must Erik have made in order to cover the cost of his hotel stay?
(Note: 1 Moroccan dirham = $0.11)

A. 1
B. 2
C. 3
D. 4

Correct Answer: D

Answer Explanation:

To stay at his fancy hotel for three nights at 2,000 Moroccan dirhams per night, Erik will need 6,000 dirhams. Using the currency conversion rate of 1 dirham = $0.11, we can multiply 6,000 × 0.11 to determine that Erik’s hotel stay will cost $660. Since his bank allows him to withdraw only $200 at a time, Erik must go to the ATM four times: (D).

8. Peter’s Petrol Station is selling regular unleaded gas for $3.49 a gallon and premium gas for $3.79 a gallon. If a car wash is purchased, then a discount of $0.10 per gallon is applied. During one morning, a total of 850 gallons of gas was sold, and 100 gallons were sold at the discounted rate. The total collected in sales was $3,016.50. Solving which of the following systems of equations yields the number of regular unleaded gallons of gas, u, and the number of premium gallons of gas, p, that were sold during that morning?

A. u + p = 850
3.49u + 3.79p = 301.65
B. u + p = 850
3.49u + 3.79p = 3,016.50
C. u + p = 850
3.49u + 3.79p = 3,026.50
D. u + p = 3,016.50
3.49u + 3.79p = 850

Correct Answer: C

Answer Explanation:

Start with the easier equation first and use Process of Elimination. The easier equation involves the total amount of gas sold.According to the question, 850 gallons of gasoline were sold, which can be expressed as u + p = 850. Eliminate (D) since it does not include this equation. The other equation in the answers is related to the amount of money collected. According to the question, $3,016.50 was collected; however, this sum included a discount of $0.10 per gallon for 100 of the gallons that were purchased or $0.10 × 100 = $10. Without the discount unleaded gas costs $3.49 and premium gas costs $3.79 a gallon, and the amount of money collected would have been $3,016.50 + $10 = $3,026.50. Only (C) provides the correct total. Therefore, the correct answer is (C).

9. Of the 784 juniors and seniors at Abingdon High School, 319 are currently enrolled in one or more Advanced Placement (AP) courses. Of these AP students, 75 are enrolled in AP Biology, 58 are enrolled in AP U.S. History, and 22 are enrolled in both AP Biology and AP U.S. History. Approximately what percent of the juniors and seniors at Abingdon High School are enrolled in AP courses other than Biology and U.S. History?

A. 17%
B. 27%
C. 37%
D. 47%

Correct Answer: C

Answer Explanation:

First, let’s figure out how many students are enrolled in AP courses other than Biology and U.S. History. We know that 319 students are enrolled in at least one AP course, and of those, 75 + 58 = 133 are enrolled in Biology and U.S. History. However, since 22 students are enrolled in both of those courses, we need to subtract 22 from 133 (so as not to double-count the students taking both courses). That leaves us with 133 – 22 = 111 total students who are taking AP Biology and AP U.S. History. Of the 319 students taking AP courses, that means there are 319 – 111 = 208 students taking AP courses other than Biology and U.S. History. We know that there are 784 juniors and seniors total, so ​\( \frac{208}{784} \)​= 0.265, or approximately 27% of all juniors and seniors, which is (B).

10. To receive a B in his chemistry class, Mateo needs to earn an average score from 80 to 89, inclusive. His grade is based only on 3 tests. The highest possible score on each of these tests is 100 points. He scored 79 on his first test and 95 on his second test. If y represents his score on the third test, which of the inequalities below shows all values of y that would earn Mateo a B in his chemistry class?

A. 66 ≤ y ≤ 93
B. 66 ≤ y ≤ 100
C. 80 ≤ y ≤ 89
D. 80 ≤ y ≤ 93

Correct Answer: A

Answer Explanation:

Total score = average score × the number of tests. In order for Mateo to receive a B, he needs his total score over the 3 tests to be between 3 × 80 = 240 points and 3 × 89 = 267 points. On his first and second tests, Mateo scored a total of 79 + 95 = 174 points. Therefore, on his third test Mateo must score between 240 – 174 = 66 and 267 – 174 = 93 points in order to receive a B. The correct answer is (A).

Pages: 1 2

Warning: Undefined variable $in_same_cat in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27

Warning: Undefined variable $excluded_categories in /www/wwwroot/mtexam.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
< PREVIOUS POST2024 SAT Standardized Test Math Practice Paper 11
NEXT POST >2024 SAT Standardized Test Math Practice Paper 13

Leave A Comment?